EJERCICIO
Puesto que la función está compuesta por un polinomio y una raíz cuyo radicando es siempre no negativo, la función es continua en los intervalos de definición. El único punto cuya continuidad debemos estudiar es x = -1
.Calculamos los límites laterales en dicho punto
Como los límites laterales no coinciden, no existe el límite de la función en dicho punto:
con lo que no puede cumplirse la definición de continuidad
.Calculamos los límites laterales en dicho punto
PROBLEMA
El dominio es todos los reales:
- En el intervalola función es continua por ser polinómica.
- En el intervalola función es continua por ser exponencial.
- En el intervalola función es continua por ser racional con el denominador distinto de 0.
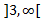
Falta estudiar la continuidad en los puntos de cambio de definición: x= 2 , 3. Para ello, calculamos los límites laterales:
Como ambos límites son distintos, no hay continuidad en x = 2.
Como los límites son distintos, no hay continuidad en x = 3.
Por tanto, la función es continua en
SOLUCIONARIO
https://drive.google.com/file/d/16dL7qJpGByu-pV4qE9htH3uIYkUTihsh/view?usp=sharing
OBJETIVOS DEL TEMA
Reconocer las condiciones para que una función sea continua en un punto y los tipos de discontinuidad que existen, además, resuelve problemas aplicados usando correctamente las propiedades.
Saber que Continuidad de una función es decir que una función f(x) es continua en un punto a, si y sólo, si se verifican las siguientes condiciones:
La función existe en a.
Existe límite de f(x) cuando x tiende a a.
El valor de la función en el punto y el límite en dicho punto son iguales
Cuando no se cumple alguna de las anteriores condiciones, se dice que la función es discontinua en el punto.
R
MATERIAL ADICIONAL
https://www.youtube.com/watch?v=H1m-N3nD2eE
REFERENCIAS BIBLIOGRÁFICAS
- Matesfacil https://www.matesfacil.com/resueltos-continuidad.htm
- hiru.eus https://www.hiru.eus/es/matematicas/continuidad-de-funciones
No hay comentarios.:
Publicar un comentario